Poker is a game of skill and strategy that has captured the imaginations of millions of people worldwide. The game is played with a standard deck of 52 cards, and the objective is to win the pot, which is the sum of money wagered by all players in a given hand. Players use many strategies to win, but one of the essential success factors is understanding probability theory. This article will explore how probability theory is used in poker, what systems are built on it, and some interesting facts and results.
Understanding Probability Theory in Poker
Probability theory is the branch of mathematics that deals with studying random events. In poker, probability theory determines the likelihood of certain events occurring. For example, what is the probability of being dealt a particular hand? Or, what is the probability of winning a hand given the cards you are holding and the cards on the table?
It is helpful to understand probability theory in poker to grasp some basic concepts. The first is the concept of odds.
Odds are a way of expressing the likelihood of an event occurring. They are usually represented as a ratio of the number of ways the event can happen to the number of ways it cannot. For example, if you are holding a pair of aces in Texas Hold’em, the odds of being dealt another ace on the flop are approximately 1 in 12.
5-card poker hands
| Hand | Distinct hands | Frequency | Probability | Cumulative probability | Odds against | Mathematical expression of absolute frequency |
|---|---|---|---|---|---|---|
Royal flush | 1 | 4 | 0.000154% | 0.000154% | 649,739 : 1 | 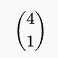 |
Straight flush (excluding royal flush) | 9 | 36 | 0.00139% | 0.0015% | 72,192.33 : 1 | 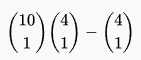 |
Four of a kind | 156 | 624 | 0.02401% | 0.0256% | 4,165 : 1 | 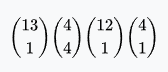 |
Full house | 156 | 3.744 | 0.1441% | 0.17% | 693.1667 : 1 | 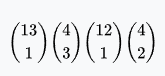 |
Flush (excluding royal flush and straight flush) | 1,277 | 5,108 | 0.1965% | 0.367% | 508.8019 : 1 | 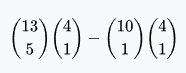 |
Straight (excluding royal flush and straight flush) | 10 | 10,200 | 0.3925% | 0.76% | 253.8 : 1 | 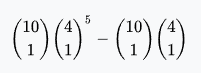 |
Three of a kind | 858 | 54,912 | 2.1128% | 2.87% | 46.32955 : 1 | 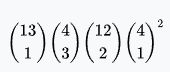 |
Two pair | 858 | 123,552 | 4.7539% | 7.62% | 20.03535 : 1 | 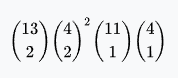 |
One pair | 2,860 | 1,098,240 | 42.2569% | 49.9% | 1.366477 : 1 | 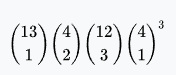 |
| High card | 1,277 | 1,302,540 | 50.1177% | 100% | 0.9953015 : 1 | |
| Total: | 7,462 | 2,598,960 | 100% | ——– | 0:1 |  |
7-card poker hands
| Hand | Frequency | Probability | Cumulative probability | Odds against | Mathematical expression of absolute frequency |
|---|---|---|---|---|---|
Royal flush | 4,324 | 0.0032% | 0.0032% | 30,940 : 1 | 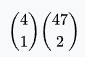 |
Straight flush (excluding royal flush) | 37,260 | 0.0279% | 0.0311% | 3,589.6 : 1 | 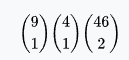 |
Four of a kind | 224,848 | 0.168% | 0.199% | 594 : 1 | 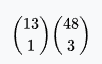 |
Full house | 3,473,184 | 2.60% | 2.80% | 37.5 : 1 | 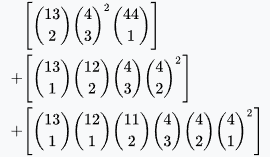 |
Flush (excluding royal flush and straight flush) | 4,047,644 | 3.03% | 5.82% | 32.1 : 1 | 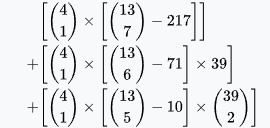 |
Straight (excluding royal flush and straight flush) | 6,180,020 | 4.62% | 10.4% | 20.6 : 1 | 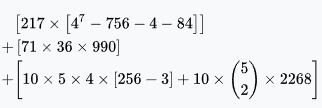 |
Three of a kind | 6,461,620 | 4.83% | 15.3% | 19.7 : 1 | 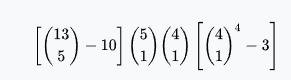 |
Two pair | 31,433,400 | 23.5% | 38.8% | 3.26 : 1 | 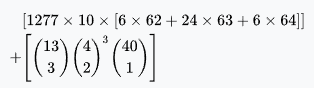 |
One pair | 58,627,800 | 43.8% | 82.6% | 1.28 : 1 | |
| High card | 23,294,460 | 17.4% | 100% | 4.74 : 1 | |
| Total: | 133,784,560 | 100% | ——– | 0:1 |  |
Another important concept in probability theory is expected value.
Expected value is a measure of the average outcome of a given event. It is calculated by multiplying the probability of each possible outcome by its value and then summing these products. For example, if you are playing a game of poker with a $100 pot and have a 50% chance of winning the pot, then the expected value is $50.
Probability theory is used in poker in many ways. One of the most common uses is determining a starting hand’s strength. A starting hand is the first two cards that a player is dealt in Texas Hold’em. The power of a starting hand is determined by its probability of winning the hand. For example, a pair of aces is more likely to succeed than a pair of twos, considered a more substantial hand.
Another use of probability theory in poker is determining the likelihood of hitting a specific hand on the flop, turn, or river. For example, if you have four cards to a flush on the flop, the probability of hitting the flush on the turn or river is approximately 35%.
Preflop probability
| Three peer cards | 0.24% |
|---|---|
| Pair +Card | 17% |
| Flop of the same suit | 5.06% |
| Two cards of the same suit | 55% |
| Cards in complete disarray | 40% |
| Straight Draw | 3.5% |
| 2 cards ascending | 40% |
| No cards in order | 56% |
Flop -> Turn probability
| Set-Full house | 15% |
|---|---|
| 2 pairs -Full house | 8.5% |
| Flesh – Flesh | 19% |
| Double side Straight Draw – Straight | 17% |
| Gutshot -Straight | 8.5% |
| Pair – Thrips | 4.5% |
| Over card – Pair | 13% |
Flop to River probability
| Set –Full house | 33% |
|---|---|
| 2 pairs -Full house | 17% |
| Flesh Draw – Flesh | 35% |
| Runner Draw -Flesh | 4.517% |
| Double side Straight Draw – Straight | 17% |
| Over card – Pair | 24% |
Probability gains on the turn and river
| Set-Full house | 22.7% |
|---|---|
| 2 pairs -Full house | 8.7% |
| Flesh Draw – Flesh | 19.6% |
| Double side Straight Draw – Straight | 17.4% |
| Straight Draw with gap | 8.7% |
| Pair – Thrips | 4.3% |
| Over card – Pair | 13% |
Probability Theory-Based Strategies in Poker
There are many different strategies that players use in poker, and many of these strategies are based on probability theory. One of the most important strategies is the concept of pot odds. Pot odds are the odds of winning the pot compared to the size of the pot. For example, if the pot is $100 and you have a 50% chance of winning, the pot odds are 2:1.
Pot odds are used to determine whether or not to make a bet or a call. If the pot odds are in your favour, making a bet or call is generally a good idea. If the pot odds are not in your favour, folding is usually better.
Another strategy based on probability theory is the concept of expected value. Expected value is used to determine whether or not a particular play is profitable in the long run. For example, if you are playing a game of poker with a $100 pot and have a 50% chance of winning the pot, then the expected value is $50. If the cost of making a bet is less than $50, then it is a profitable play in the long run
Another strategy based on probability theory is the use of position. Position refers to a player’s position relative to the dealer button. The player who acts last has the most information about the other players’ actions and can make better decisions based on that information. It is because they can see what the other players do before they have to act. Players in earlier positions need more information and are at a disadvantage. Therefore, players in later positions can use their position to bluff or make aggressive plays with weaker hands, while players in earlier positions need to be more cautious.
The concept of implied odds is also based on probability theory. Implied odds are the odds of winning a hand, including the potential future bets that could be won if the hand improves. For example, if you have a flush draw on the flop, the pot odds may not be in your favour, but the implied odds may be high if you think you can win a large pot if you hit your flush.
In this example, we’ll calculate the probability of getting a specific poker hand, such as a flush, using Python. We’ll use the itertools module for combinations:
| import itertools import collections def poker_probability(hand_rank): suits = ‘CDHS’ ranks = ‘23456789TJQKA’ deck = [r + s for s in suits for r in ranks] def is_flush(hand): return len(set(suit for _, suit in hand)) == 1 def is_four_of_a_kind(hand): count = collections.Counter(rank for rank, _ in hand) return any(val == 4 for val in count.values()) hand_checks = { ‘flush’: is_flush, ‘four_of_a_kind’: is_four_of_a_kind, } if hand_rank not in hand_checks: raise ValueError(f”Invalid hand rank ‘{hand_rank}'”) total_hands = 0 desired_hands = 0 for hand in itertools.combinations(deck, 5): total_hands += 1 if hand_checks[hand_rank](hand): desired_hands += 1 probability = desired_hands / total_hands return probability hand_rank = ‘flush’ print(f”The probability of getting a {hand_rank} is: {poker_probability(hand_rank):.6f}”) |
In this example, we have a function poker_probability that calculates the probability of a given poker hand rank. It checks for flushes and four-of-a-kind hands, but you can extend it by adding more hand checks (e.g., straight, full house, etc.). The function uses itertools.combinations to iterate through all possible 5-card hands, and it checks if the current hand meets the desired hand rank criteria.
To use the code, set the hand_rank variable to the desired poker hand rank (e.g., ‘flush’, ‘four_of_a_kind’) and run the script. The probability of obtaining the specified hand will be displayed as output. Note that calculating probabilities for all 2,598,960 possible 5-card hands can take some time.
Finally, the use of hand ranges is a strategy that is based on probability theory. A hand range is a set of possible hands that a player can have based on their actions and the cards that have been revealed. By analyzing the hand range of the other players, a player can make better decisions about what hands to play and what hands to fold.
Interesting Facts and Results
There are many interesting facts and results related to probability theory in poker. One of the most interesting is the concept of the “nuts.” The nuts are the best possible hand that can be made with the cards on the table. Knowing the nuts is important because it allows a player to make better decisions about whether or not to continue betting. For example, if a player has the nuts, they can be more confident in their bet, knowing they have the best hand.




In poker, “nuts” refers to the best possible hand that can be made with the cards on the table. Knowing the nuts is an integral part of playing poker, as it allows a player to make better decisions about whether to bet, call, or fold.
The nuts strategy involves identifying the best possible hand that can be made with the cards on the table and then betting aggressively if you have it or folding if you don’t. The strategy is based on the idea that you will likely win the hand if you have the nuts, and if you don’t, you will lose.
To identify the nuts, a player must analyze the community cards on the table and consider all possible combinations of cards that could be used to make a hand. For example, in Texas Hold’em, if the community cards are 5-6-7-8-9 and you have a 10-J, then you have the nuts with a straight.
Once the nuts have been identified, the player can use this information to decide whether to bet, call, or fold. If the player has the nuts, they can be more confident in their bet, knowing they have the best possible hand. They may choose to make a large bet to maximize their winnings.
If the player doesn’t have the nuts, they may choose to fold, especially if facing a large bet. It is because they are very likely to lose their hand if they continue to play, and it is not worth risking their chips on a losing hand.
However, the nuts strategy could be better, as there is always the possibility that another player has a better hand. It is known as getting “counterfeited,” where the community cards improve and make a better hand than the one the player thought they had. Therefore, it is vital to re-evaluate the nuts as the writing progresses continually and to be prepared to adjust your strategy if necessary.
In conclusion, the nuts strategy in poker involves identifying the best possible hand that can be made with the cards on the table and using this information to make decisions about whether to bet, call, or fold. While not foolproof, it can be a powerful tool in a player’s arsenal and help increase their winnings over time.
Another interesting result related to probability theory is the concept of the “Monte Carlo method.” The Monte Carlo method is a computational algorithm used in poker to simulate the outcome of a hand based on the probability of different events occurring. This method determines the probability of winning a hand based on the cards on the table and the cards in a player’s hand.
The Monte Carlo method generates many random scenarios to simulate the outcome of a hand. Each scenario is developed by randomly selecting cards from the remaining deck and then using those cards to create a possible hand for each player. This process is repeated many times to generate a large sample size of possible hands.
Once the possible hands have been generated, the Monte Carlo method simulates the action in the hand based on different strategies and activities the players may take. For example, the algorithm may affect betting patterns, such as a player making a small bet or going all-in.
After simulating the action in the hand, the Monte Carlo method determines the probability of winning the hand for each player based on the possible hands generated in the first step. This probability is calculated by dividing the number of simulations where a player won the hand by the total number of simulations run.
The Monte Carlo method is helpful in poker because it allows players to analyze the probability of winning a hand based on different scenarios and betting patterns. It can also determine the expected value of a particular play or decision.
For example, suppose a player has a pair of aces in Texas Hold’em and faces a large bet from another player. Using the Monte Carlo method, the player could simulate the outcome of the hand based on different scenarios, such as whether the other player is bluffing or has a firm hand. Based on these scenarios, the player could then determine the probability of winning the hand and decide whether to call, fold, or raise.
In conclusion, the Monte Carlo method is a powerful tool in poker that allows players to simulate the outcome of a hand based on the probability of different events occurring. This method can determine the likelihood of winning a hand, analyze different scenarios and betting patterns, and decide whether to call, fold, or raise.
Finally, many different probability distributions are used in poker. The most common are the normal distribution, the binomial distribution, and the Poisson distribution. These distributions are used to model the probability of different events occurring in a poker game.
Conclusion
Probability theory is an essential part of poker. It is used to determine the strength of a hand, the likelihood of hitting a particular hand, and the probability of winning a hand. Probability theory also develops many strategies, including pot odds, expected value, position, implied odds, and hand ranges. There are many interesting facts and results related to probability theory in poker, including the concept of the nuts, the Monte Carlo method, and different probability distributions. Overall, understanding probability theory is essential for success in poker.








