Roulette, a classic game of chance, frequently raises questions about the potential for long-term winnings. In this article, we delve into the mathematical intricacies of the game to shed light on the odds and potential outcomes for players.
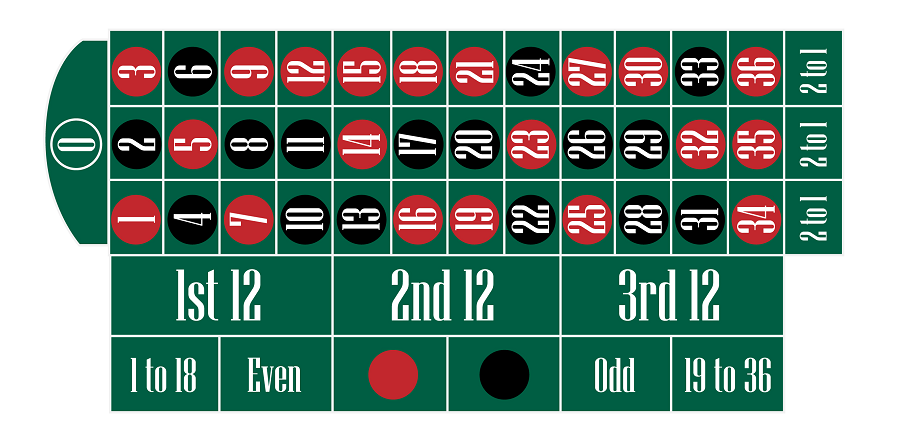
Pic. 1 – European Roulette table
Roulette allows players to place bets on individual numbers or clusters of numbers, and each type of bet carries its distinct payout.
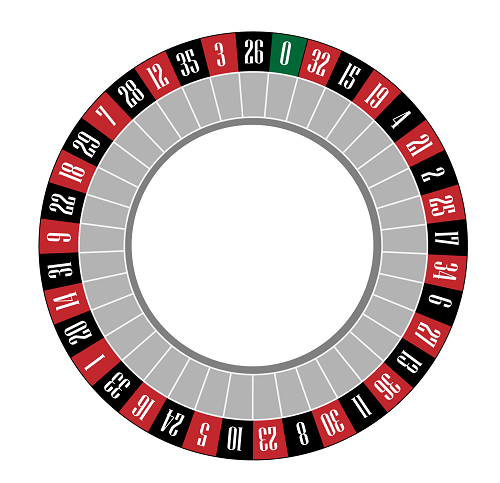
Pic. 2 – European Roulette
In standard European Roulette
• There are 18 red numbers and 18 black numbers, totaling 36, and a green zero, resulting in 37 numbers in total.
• Half of these 36 numbers are even, while the other half are odd. The number 0 or 00 is neutral, being neither even nor odd.
It’s worth noting that American Roulette features an additional number, the double zero. However, for the scope of this discussion, our focus will remain on European Roulette, which has a single zero.
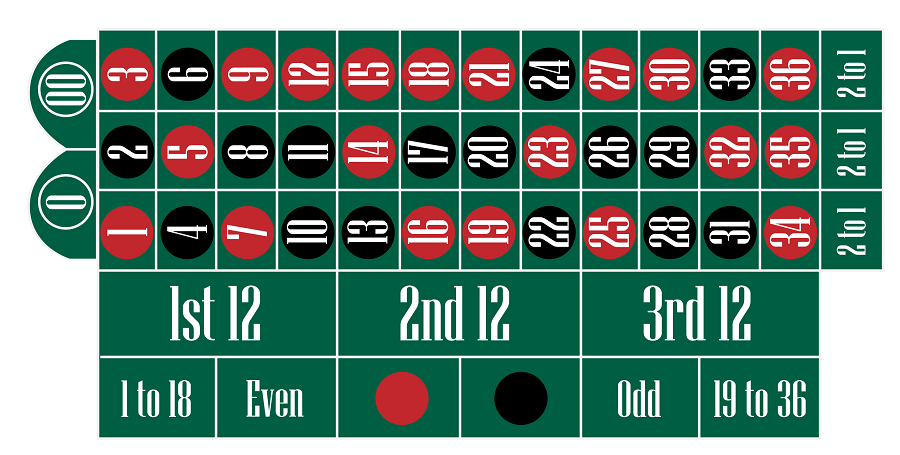
Pic. 3 – American Roulette table
Bets can be placed when the roulette wheel is stationary or spinning until the dealer (or machine) announces, “No more bets.” Once the ball settles on a number, winners receive rewards, while the dealer collects chips from those who did not correctly predict the outcome.
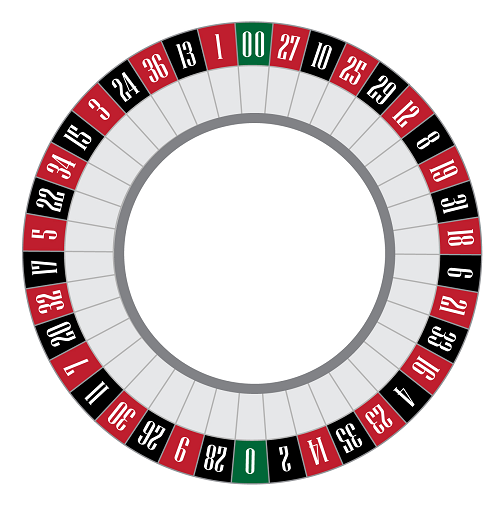
Pic. 4 – American Roulette
Types of Roulette Bets and their Probabilities
Simple Bet:
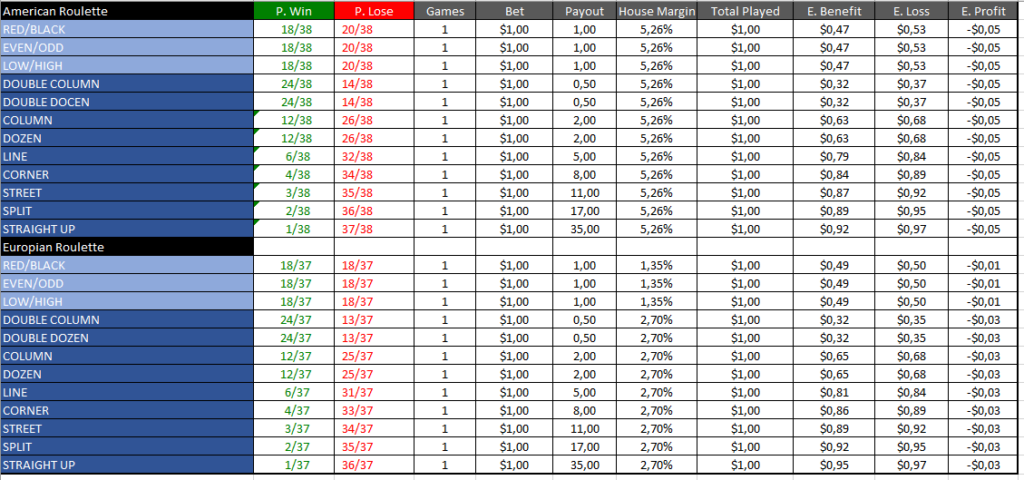
• Red/Black: Payout is 1 to 1 with a probability of 18/37 (~48.6%).
• Even/Odd: Payout is 1 to 1 with a probability of 18/37 (~48.6%).
• Low-High (1-18/19-36): Payout is 1 to 1 with a probability of 18/37 (~48.6%).
Multiple Bets
• Double Dozen: Payout is 1/2 to 1 with a probability of 24/37 (~64.8%).
• Double Column: Payout is 1/2 to 1 with a probability of 24/37 (~64.8%).
• Dozen: Payout is 2 to 1 with a probability of 12/37 (~32.4%).
• Column: Payout is 2 to 1 with a probability of 12/37 (~32.4%).
• Line/6 number: Payout is 5 to 1 with a probability of 6/37 (~16.2%).
• Corner: Payout is 8 to 1 with a probability of 4/37 (~10.8%).
• Street: Payout is 11 to 1 with a probability of 3/37 (~8.1%).
• Split: Payout is 17 to 1 with a probability of 2/37 (~5.4%).
• Straight Up: Payout is 35 to 1 with a probability of 1/37 (~2.7%).
For comparison’s sake, percentages for American Roulette are also provided, though they are slightly lower due to the inclusion of the double zero.
Upon analysis, it becomes clear that the payout varies while the mathematical probability remains consistent between Simple and Multiple bets. Specifically, higher-risk bets offer more substantial rewards.
It presents two critical questions:
1. Are the payouts sufficiently lucrative to justify the risks?
2. Between high-probability, low-reward bets and low-probability, high-reward bets, which offers the best strategy for players?
Mathematical Analysis of Roulette
When viewed from a mathematical perspective, any roulette bet can be conceptualized as a binary experiment with two outcomes: success or failure. Intriguingly, the probability of landing on a given number remains consistent regardless of the specific numbers selected. This uniformity arises because each number has an equal chance of being selected.
Importantly, each spin of the roulette wheel is independent of prior spins; the outcome of a previous game has no bearing on subsequent rounds.
To determine the profitability of a bet, one needs to understand its expected value or average profit. Thus, we first define the term mathematical expectation.
For a binomial variable, the expectation represents the average number of successful outcomes in nn trials and is calculated as p⋅np⋅n. In the context of Roulette, this would signify the average number of bets won when playing nn times.
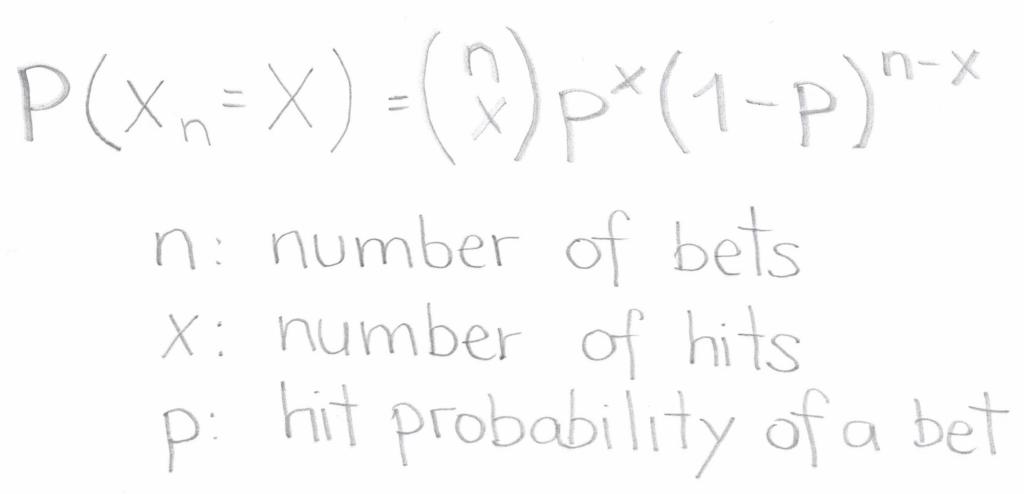
The expectation of a Straight Up Bet: For a single number bet, the anticipation for one game is 1×(1/37)1×(1/37), which equates to approximately 0.027. It suggests that when betting on a single number once, there’s a 2.7% chance of a successful outcome on average. If one were to play two games, the expectation doubles to 5.4%, and so on. Notably, for 37 games, the expectation is 1, indicating that, on average, betting on a single number 37 times results in one win, an intuitive conclusion for some players.
Profit Expectation of a Straight-Up Bet: To calculate the expected profit for a bet, one must consider the average number of hits for that bet and its payout.
Expected profit=Expected Benefit−Expected loss expected profit=Expected benefit−Expected loss.
Where: Expected benefit=Expectation (of the bet)×payout×betExpected benefit=Expectation (of the bet)×payout×bet Expected loss=Loss Expectation (of the bet)×payout×betExpected loss=Loss Expectation (of the bet)×payout×bet
For a Straight Up bet in one game: Expected profit=137×35(payout)×bet−3637×betExpected profit=371×35(payout)×bet−3736×bet
This calculation yields an expected profit of about -0.027. Thus, for a single bet, one can anticipate an average loss of 2.7% of the chance. Correspondingly, the casino’s edge or house advantage is 2.7% of the bet for each game. If extended over two games, the casino’s advantage amplifies to 5.4%.

Expanding this to 37 games: while one might expect to win once, the net gain or loss becomes crucial. Given that there’s one expected win and 36 expected losses over 37 games, the calculations show an expected profit of −1×bet−1×bet. It implies that over 37 games, the casino anticipates winning, on average, the value of one bet. If one were to consistently bet $1 on a single number over 37 games, they would, on average, lose $1
Expectations of Profit Across Different Roulette Bets
From our analysis, wagering on a Straight is unprofitable both in the short and long term. Statistically, as one increases their bets, their losses escalate. On average, it takes 37 games to secure a win on a single number, only to be rewarded with a payout of 35 chips. It is less than the total wagered, making the Straight bet seemingly inadvisable.
Considering this, one might ponder: are there more profitable alternatives to the Straight bet? It’s essential to analyze the profit margins across various bets to address this. I have performed extensive calculations to elucidate this, which I present below:
Simple Bets:
• Red-Black: 1837Ap−1937Ap3718Ap−3719Ap = −174Ap−741Ap or approximately -1.35% of the bet.
• Even-Odd: 1837Ap−1937Ap3718Ap−3719Ap = −174Ap−741Ap or approximately -1.35% of the bet.
• Low-High: 1837Ap−1937Ap3718Ap−3719Ap = −174Ap−741Ap or approximately -1.35% of the bet.
Multiple Bets:
• Double Column: 1237Ap−1337Ap3712Ap−3713Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Double Dozen: 1237Ap−1337Ap3712Ap−3713Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Column: 2437Ap−2537Ap3724Ap−3725Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Dozen: 2437Ap−2537Ap3724Ap−3725Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Line/6 Number: 3037Ap−3137Ap3730Ap−3731Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Corner: 3237Ap−3337Ap3732Ap−3733Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Street: 3437Ap−3537Ap3734Ap−3735Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Split: 3337Ap−3437Ap3733Ap−3734Ap = −137Ap−371Ap or approximately -2.70% of the bet.
• Straight Up: 3537Ap−3637Ap3735Ap−3736Ap = −137Ap−371Ap or approximately -2.70% of the bet.
Utilizing a spreadsheet, I’ve applied these formulas to each type of bet, factoring in their respective probabilities and payouts, enabling an analysis of profits across multiple rounds. The pivotal insight from these computations is that both simple and various bets yield the same expected profit in European Roulette and similarly in American Roulette. This consistency in European Roulette is mainly due to the rule where a bet only loses half its value if a 0 is rolled, making returns more favourable.
Key Takeaways
1. Simple bets offer better returns than Straights or any multiple bets.
2. The exact bet choice is inconsequential Within both simple and multiple bets. Opting for two dozen increases win frequency, but losses are steeper when they do occur. Conversely, while a Straight offers a higher payout, the actual investment outweighs potential returns, explaining why the house margin remains consistent across all bets
Simulation Using Real Currency
Consider the following simulation illustrating potential outcomes using real currency:
• one game betting $1 or €1: On average, in simple bets, you’d lose 1 cent, while in multiple bets, you’d lose nearly 3 cents. It is because in simple bets if a 0 is rolled, only half the bet is lost.
• one game betting $20 or €20: In simple bets, the loss averages 27 cents, while in multiple bets, it’s 54 cents. Thus, larger bets correlate with more significant losses.
• 20 games betting $1 or €1 each: The loss remains 27 and 54 cents. It means betting $20 in a single game versus $1 across 20 games yields similar results. However, the more games you play, your losses become more consistent.
• 37 games of any bet amount: On average, in multiple bets, the entire bet amount is lost, while in simple bets, only half is lost. In essence, by knowing the bet amount (x), you can predict the average loss for any bet.

Do note these outcomes are specific to European Roulette. American Roulette has worse odds because of an additional number. If a 0 or 00 is rolled, all bets are lost.
Questions from readers
Question: If a series has had many reds, is a black more likely in the next roll?
Answer: No. It is a common misconception. Roulette is a physical system without memory. Each spin is independent of previous results. While sequences of reds or blacks may seem unusual, each spin retains the same probability, but please read this article as well.
Question: What if I place several bets simultaneously, like betting on multiple numbers?
Answer: Combining bets involves making several bets simultaneously but they must be interconnected. Each bet is evaluated and paid out separately. While covering more numbers increases your probability of winning, it doesn’t enhance profitability. More simultaneous bets only mean more non-profitable bets, reducing overall profitability.
Question: What happens if I double my bet every time I lose?
Answer: This strategy, known as the “martingale,” has its pitfalls. It’s crucial to consider your chip count and how many times you can afford to double your bet. Doubling means progressively larger chances after each loss. Consistent losses result in exponential bet growth, potentially depleting your funds rapidly. Long sequences of one colour are rare but possible. The longer you play, the more likely such a sequence occurs, potentially causing significant losses.
Question: You mentioned the margin remains consistent for multiple plays, but are there differences?
Answer: Yes, there are nuances. Opting for low-probability bets, like a Straight, will result in more frequent losses, prompting more games to recoup losses. The more you play, the more you stand to lose.
Question: With a limited number of chips, which bet is advisable?
Answer: Avoid low-probability bets, such as a Straight for limited chips. For a straight-up bet, an average of 37 spins is needed for a hit. With enough chips, chances are you’ll run out before hitting. Opt for single or high-probability bets.
Question: I’m surprised that a single $20 game equals 20 rounds of $1. Why not play more fun with the same money?
Answer: Statistically, you’d average the same earnings. However, averages are based on large sample sizes. Playing more times allows your results to converge to this average, while a single game can result in more volatile outcomes. Casinos offer chips for set amounts to encourage multiple plays, allowing mathematics to dictate results.
Question: If I play with those $20 one chip at a time, will I lose more money?
Answer: Not necessarily more money, but with a higher certainty, you will converge to the expected negative outcome. However, this also means you are less likely to deviate significantly from that amount, either positively or negatively. Over the long term, any deviations are corrected, bringing you closer to the expected outcome, which is unfavourable. Thus, the more you play, the harder it becomes to profit.
Question: Are you suggesting that the casino prefers players to bet multiple times, even with the same total stake?
Answer: Precisely. The more times you play, the less chance a lucky streak will be in your favour.
Question: Should I place the entire $20 on a single bet if I aim to profit?
Answer: If you want to maximize potential gain on one instance, yes. Betting the $20 in one go means winning or losing that entire sum in that single bet. You’d need a consecutive win (or loss) streak to achieve the same outcome by playing with smaller increments. It’s one thing to hit (or miss) once and entirely another to hit (or miss) multiple times consistently.
Question: True, but isn’t it also riskier since it’s easier to miss once than four times consecutively?
Answer: More significant risks can lead to greater rewards or losses. Conversely, the more conservative approach yields outcomes with higher predictability, albeit statistically unfavourable in the long run.
Final Thoughts
Roulette isn’t a sustainable means to profit:
• Casinos don’t need to manipulate the game; the inherent odds are already against players.
• The only feasible way to profit from Roulette is by leveraging some physical phenomena or statistical anomalies specific to a table. It would require extensive data collection on tens of thousands of spins and rigorous mathematical analysis.
However, caution is advised. If a particular number appears more frequently, it’s more likely due to chance than an actual higher probability for that number. Casinos consistently strive to ensure their games remain as random as possible. One could extensively study numerous spins to understand this better for those curious.
Should you choose to play, here are some recommendations:
• Stick to straightforward, higher-probability bets.
• Play infrequently and limit the number of bets.
• Avoid combining bets.
• Set a strict budget before playing and adhere to it.
• Know when to quit. Trust me on this one.
Over the long haul, keep these principles in mind:
• The more money wagered, the more the casino profits.
• Combining bets increases the casino’s advantage.
• The more frequently you play, the more predictable (and unfavourable) your outcomes become.
Does the house always come out on top? While the casino might not always win in the short term, it invariably comes out ahead over multiple visits. The game, after all, is never truly over.








